单因素统计分析方法

医路糜语

单因素方差分析是指对单因素试验结果进行分析，检验因素对试验结果有无显著性影响的方法。通常只描述某一变量的统计特征，并对该变量在各组间的差别进行比较，是一种最简单的定量统计分析，其基本方法是通过描述样本中研究对象某一变量的各种属性，来绘制该变量的数分布图，以便根据资料分布情况选择合适的统计方法作进一步的统计分析。与之相对的是多因素方差分析，既当有两个或两个以上因素对变量产生影响时所采用的分析方法。

一、单因素分析的步骤

为了便于分析，可以将方差分析分解为提出原假设和备择假设、确定检验的统计量、决策分析等步骤。

1. 提出假设

在方差分析中，原假设所描述的是：在按照白变量的值分成的类中，因变量的均值是否相等

2. 计算检验统计量

由方差分析原理可知，原假设是否为真由剔除自由度影响的组间均方差和组内均方差的相对比决定，因此，在计算F统计量之前必须确定各种方差的自由度。

3. 统计决策

计算出检验统计量后，将检验统计量的值F与给定的显著性水平α的临界值Fα进行比较，从而做出对原假设地的决策。

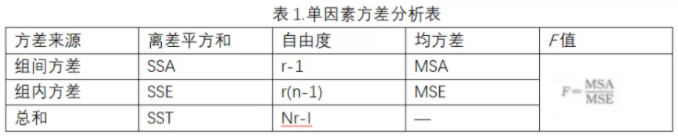
前面详细介绍了方差分析的计算步骤，为了使计算过程清晰，常将计算结果排列于一张表中，形成方差分析表，如表1.

二、单因素方差分析的进一步分析

1. 方差齐性检验

在完成单因素方差的基本分析后，可得到关于控制变量是否对观测变量造成显著影响，因为在方差分析前，我们假定各个总体的方差必须相等，所以我们须对方差是否齐性进行检验。 SPSS单因素方差分析中，方差齐性检验(homogeneity of variance)采用了同质性检验方法，其原假设是：各水平下观测变量总体的方差无显著差异，与SPSS两独立样本t检验中的方差检验一样。

2. 多重比较检验

方差分析可以对若干平均值是否相等同时进行检验，看它们之间是否存在显著的区别。如果检验结果拒绝原假设，仅仅表明检验的这几个均值不全相等，至于是哪一个或哪几个均值与其他均值不等，前面所进行的分析并没有告诉答案。如果要对此问题进一步分析，就需要采用一些专门的方法，通常被称为方差分析中的多重比较检验。多重比较检验的原理是：利用全部观测变量。实现对各个水平下观测变量总体均值的两两比较。这与两独立样本假设原理一样，因此遵循假设检验的基本步骤。当然，如果对两两之间进行检验，问题就复杂了。 SPSS提供了许多多重比较检验的方法，其差异主要体现在检验统计量的构造上，有些适用于各总体方差相等的条件，有些则适用于方于方差不等的条件。